Rasterizace objetů #2: Bresenhamův algoritmus

Rasteriace je proces, při kterém převádíme základní grafické objekty do systému posloupnosti obrazových bodů. Toto je důležité při práci s různými výstupními zařízeními, které nejsou schopny zobrazit přesně daný objekt, ale při svém zobrazení používají rastr.

V minulém článku jsme si řekli o DDA algoritmu, v tomto, druhém pokračování, se podíváme na Bressahamův algoritmus pro generování úsečky.

Breansshamův algoritmus funguje na principu hledání nejbližších bodů, které leží k úsečce.
Mějme bod, jehož souřadnice jsou Xi a Yi. Bod representuje počáteční bod úsečky, kterou se snažíme vykreslit.

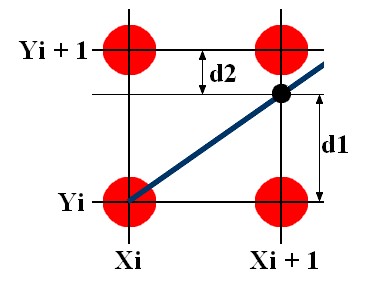
Víme že úsečka pokračuje doprava směrem nahoru, takže je jasné, že souřadnice X_i+1 bude o hodnotu 1 větší, ale souřadnici Y_i+1 neznáme. V podstatě máme dvě možnosti, který ze dvou bodů zvolit. Můžeme volit bod, který je shodný s bodem Yi, nebo můžeme volit bod Y_{i + 1}:

[X<sub>i+1</sub>, Y<sub>i</sub>] nebo [X<sub>i+1</sub>, Y<sub>i+1</sub>]

1	[X<sub>i+1</sub>, Y<sub>i</sub>] nebo [X<sub>i+1</sub>, Y<sub>i+1</sub>]

Jak je vidět na obrázku, bod, který leží blíže úsečky můžeme určit pomocí hodnot d1 a d2:

Δd = d<sub>1</sub> – d<sub>2</sub>

1	Δd = d<sub>1</sub> – d<sub>2</sub>

Pokud d < 0: hodnota následujícího pixelu je Y_i

Pokud d > 0: hodnota následujícího pixelu je Y_i+1

m =   ΔY/ ΔX
b = ((X2*Y1) – (X1*Y2))/(X2-X1)
d<sub>1</sub> = m (x<sub>i + 1</sub>) + b - yi
d<sub>2</sub> = y<sub>i + 1</sub> - m (x<sub>i + 1</sub>) - b

m = ΔY/ ΔX

b = ((X2*Y1) – (X1*Y2))/(X2-X1)

d1 = m (xi + 1) + b - yi

d2 = yi + 1 - m (xi + 1) - b

Iteračním způsobem můžeme počítat hodnoty další souřadnice:

k =   Δx/ Δ y
e1 = 2  Δy -  Δx

1 2	k = Δx/ Δ y e1 = 2 Δy - Δx

Pro ei+1 platí:

e<sub>i</sub> > 0 : e<sub>i+1</sub> = e<sub>i</sub> + 2 Δy - 2 Δx
ei <= 0: ei + 1 = ei + 2 Δy

1 2	e<sub>i</sub> > 0 : e<sub>i+1</sub> = e<sub>i</sub> + 2 Δy - 2 Δx ei <= 0: ei + 1 = ei + 2 Δy

Zdrojový kód v jazyce java může vypadat například takto:

public static void line(int x1,int y1,int x2, int y2 ) {
    int w = x2 - x1;
    int h = y2 - y1;
    int dx1 = 0, dy1 = 0, dx2 = 0, dy2 = 0 ;
    if (w<0)
        dx1 = -1;
    else if (w>0)
        dx1 = 1;
    if (h<0)
        dy1 = -1;
    else if (h>0)
        dy1 = 1;
    if (w<0)
        dx2 = -1 ;
    else if (w>0)
        dx2 = 1 ;
    int longest = Math.abs(w);
    int shortest = Math.abs(h);
    int numerator = longest >> 1;
    for (int i=0;i<=longest;i++){
        System.out.println(x1 + " " + y1);
        numerator += shortest;
        if (!(numerator &gt; longest)) {
            numerator -= longest;
            x1 += dx1;
            y1 += dy1;
        } else {
            x1 += dx2;
            y1 += dy2;
        }
    }
}

public static void line(int x1,int y1,int x2, int y2 ) {

int w = x2 - x1;

int h = y2 - y1;

int dx1 = 0, dy1 = 0, dx2 = 0, dy2 = 0 ;

if (w<0)

dx1 = -1;

else if (w>0)

dx1 = 1;

if (h<0)

dy1 = -1;

else if (h>0)

dy1 = 1;

if (w<0)

dx2 = -1 ;

else if (w>0)

dx2 = 1 ;

int longest = Math.abs(w);

int shortest = Math.abs(h);

int numerator = longest >> 1;

for (int i=0;i<=longest;i++){

System.out.println(x1 + " " + y1);

numerator += shortest;

if (!(numerator > longest)) {

numerator -= longest;

x1 += dx1;

y1 += dy1;

} else {

x1 += dx2;

y1 += dy2;

}

Zdrojový kód převzat: http://tech-algorithm.com/index.php?post=30

Závěrem:

Oproti DDA algoritmu nabízí Bresenhamův algoritmus velké zrychlení, co do počítání souřadnic pro výpis hodnot.

Velkou výhodou, kterou nám Breasshamův algoritmus umožňuje, je snadný převod do celočíselné aritmetiky, který velmi zjednodušuje výpočty.

Comments are closed for this page

WhiteHat

05/05/2010

A co výběr řídící osy?

nginx

15/01/2015

Hello there! Quick question that’s totally off topic. Do you know how to make your site mobile friendly? My site looks weird when viewing from my iphone 4. I’m trying to find a theme or plugin that might be able to resolve this problem. If you have any suggestions, please share. Many thanks!|

Terrell Barlett

10/03/2016

Oh my goodness! Amazing article dude! Thank you so much, However I am going through issues with your RSS. I don know the reason why I can’t subscribe to it. Is there anyone else getting the same RSS problems? Anyone who knows the solution will you kindly respond? Thanks!!